Title: Supervised Convex Clustering
Authors & Year: Minjie Wang, Tianyi Yao, and Genevera I. Allen (2023)
Journal: Biometrics [DOI: 10.1111/biom.13860]
Review Prepared by Edmond Sanou
Clustering is a common way for computers to group together similar things when we don’t already know the categories. The problem is that the groups it finds are sometimes hard to make sense of. In real life, though, we often have extra pieces of information, like doctors’ opinions or other clues, that, while imperfect, can help guide the grouping. The authors Wang, Yao, and Allen. created a new method called supervised convex clustering (SCC), which combines both the raw data and these extra guiding clues. This makes the discovered groups easier to interpret and more meaningful scientifically. They also adapted the method so it can handle different kinds of extra information and even look for patterns in two dimensions at once (biclusters). When they tested SCC, including on Alzheimer’s disease genetic data, it not only confirmed useful patterns but also revealed new possible genes and subtypes of Alzheimer’s disease. These findings could help researchers better understand why the disease affects people differently.
Unsupervised clustering
Unsupervised clustering, commonly referred to as clustering, is a way of exploring data by grouping together items that are similar, without making assumptions about how the data is structured. The challenge is that we often don’t know in advance what patterns we’re looking for, or whether the patterns we find are truly meaningful. For example, in medical research, an ideal result would be that the groups consist of the different ways that patients respond to a disease. But the signal of interest might be very weak, hidden by noise, or lost due to technical issues in the data. Because there’s no “true” answer to compare against, it’s hard to be sure if the discovered groups are scientifically useful or just artifacts of the data. There are many types of clustering algorithms, and each works by following a different rule for grouping data, like making items inside a group as similar as possible. Because they use different rules, the results can vary depending on the method chosen. Well-known methods include k-means, hierarchical clustering, and Gaussian mixture models. A newer and less common family, called convex clustering methods, is now gaining attention.
Supervised clustering
Normally, clustering is done without any guidance, and researchers later check whether the groups make sense using extra information (like patient outcomes or other data). The authors call these extra pieces of information “supervising auxiliary variables”. Their idea is to actually include these variables in the clustering process itself, so the groups formed are more accurate and easier to interpret. This approach is different from supervised learning, where the extra data is treated as absolute truth. Here, the auxiliary variables are seen as imperfect clues, helpful but noisy, so they are used to guide the clustering without completely dictating it.
Convex clustering
Traditional clustering methods like k-means, Gaussian mixtures, and hierarchical clustering can find different shapes of groups, but they often give unstable results because of the way the math is set up. To address these issues, researchers developed convex clustering, which applies a mathematical framework called convex optimization. This approach makes the results more reliable, stable, and consistent. Unlike traditional methods, convex clustering solves the clustering problem across a range of penalization parameters independently, ensuring the best possible grouping. Because the problem is convex, the final solution does not depend on how the algorithm is initialized.
Convex clustering borrows ideas from the fused Lasso, where a penalty function (sum of the absolute values of the differences between coefficients) is applied to shrink differences between neighboring coefficients toward zero. Each subject is represented by a “center” (centroid). if two centroids become identical, their corresponding subjects are assigned to the same cluster.
The optimization problem minimizes a combination of two things:
- Clustering loss: the sum of distances between each observation and its centroid.
- Fusion penalty: the sum of L1 or L2 norms of the differences between centroids (as in the fused Lasso or fused group Lasso), encouraging centroids to merge.
A tuning parameter balances these terms: weak penalties keep many small clusters, while stronger penalties fuse them into fewer, larger clusters, until eventually all observations belong to one cluster.
Supervised convex biclustering
The authors propose a new way of clustering that combines two sources of information: the raw (unlabeled) data and extra guiding variables (the “supervising auxiliary variables”). They extend convex clustering by linking these two parts through a shared penalty term, which pushes them to form the same group structure. The idea works like this: for individuals to be placed in the same cluster, there must be consensus from both raw data and the auxiliary variables. A special penalty (inspired by the group lasso method) gradually merges subjects with similar centers into the same cluster.
The novelty of this penalty is that it forces the raw data and the auxiliary variable to agree on the groupings, producing clusters that are both data-driven and guided by the auxiliary information.
To group both observations and features at the same time, the authors extended their method to a biclustering approach. Biclustering allows finding clusters not only among the subjects but also among the features (like genes), so that patterns shared by specific groups of subjects and features can be identified simultaneously.
Application on Alzheimer’s disease data
One key application of the proposed method is in clinical genomics, where the goal is to understand the genetic basis of diseases and identify potential biomarkers for personalized treatments. Personalized medicine often requires finding groups of patients with similar genetic profiles and similar clinical outcomes, for example, breast cancer patients with different genomic subtypes receive different treatments.
In this case study, the authors apply their supervised convex clustering (SCC) method to study Alzheimer’s Disease (AD), a brain disorder that gradually damages cognitive abilities. Older adults show a lot of variation in cognition, and the genetic causes of AD are still largely unknown. Using a dataset of 507 subjects and over 41,000 genes, the authors combine clinical measurements and gene expression data. As a guiding clue, they use the global cognition score, a summary of 19 cognitive tests taken near death, where higher scores indicate better cognitive function.
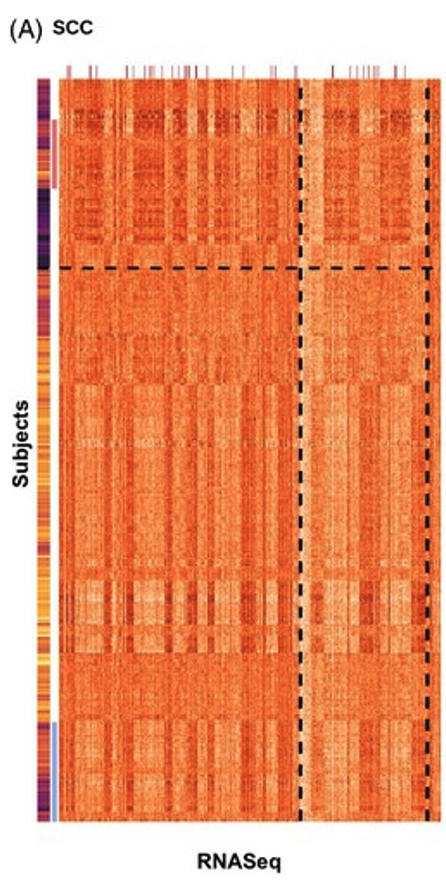
The heatmap shows that the top cluster (above the horizontal dashed line) mostly contains subjects with lower cognition scores, while the bottom cluster mostly contains subjects with higher cognition scores. For simplicity, the authors refer to these as the “low cognition cluster” and “high cognition cluster.” Looking at the gene expression patterns in these clusters, the SCC method reveals clear differences in many genes between the low and high cognition groups. These differences suggest potential genetic biomarkers that might influence cognitive decline and the development of Alzheimer’s Disease.
