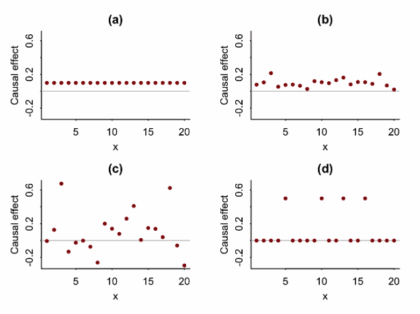
More than averages: using causal quartets to illustrate variability
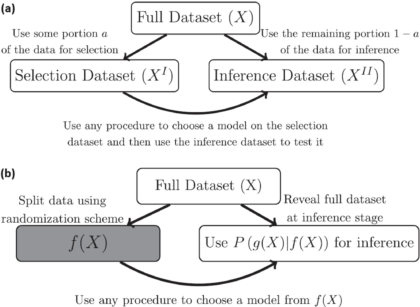
Article Title: Causal Quartets: Different Ways to Attain the Same Average Treatment Effects [DOI:10.1080/00031305.2023.2267597]Authors & Year: A. Gelman, J. Hullman, and L. Kennedy (2023)Journal: The American StatisticianReview Prepared by Peter A. Gao Causal inference research commonly focuses on estimation of average treatment effects: In a target population, what is the difference in mean outcomes between individuals who receive the treatment and individuals who receive a control? For example, imagine an experiment investigating whether limiting daily phone usage improves academic performance among high school students. Subjects are randomly sorted into a treatment group (limited to one hour of phone time daily) or a control group (unrestricted) and over the course of a semester, their academic performance is measured using exams. In this case, the average treatment effect is simply the average exam score of the treated students minus the average score of the control students. If this effect is large and…
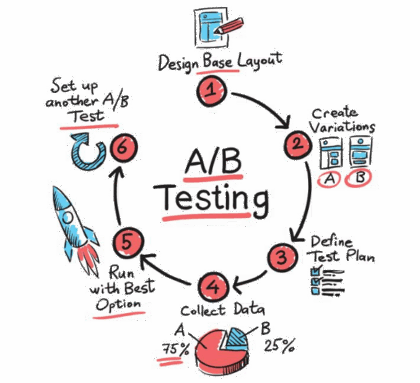
The Power of Online Experiments – What Big Tech Can Teach Us About Testing Ideas
Article Title: Statistical Challenges in Online Controlled Experiments: A Review of A/B Testing Methodology Authors & Year: Larsen, N., Stallrich, J., Sengupta, S., Deng, A., Kohavi, R., Stevens, N.T. (2024) Journal: The American Statistician [DOI: 10.1080/00031305.2023.2257237]Review Prepared by David Han What’s an Online Experiment & Why Should We Care? Have you ever wondered how Netflix decides what thumbnails to parade on your screen, or how Amazon chooses what items to nudge into your recommendations? Behind the scenes, many of these choices come from something known as A/B testing, a type of experiment that companies rely on to make smart, data-driven decisions. Picture this: After creating two versions of a webpage, you deploy each site to separate groups of users online. You then patiently wait to see which one performs better – say, attracting more clicks or garnering more purchases. This is an A/B test in action. In the tech world,…
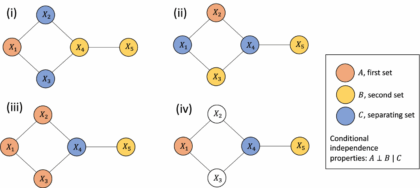
How can Gaussian graphical Networks Models help in exploring Ovarian cancer data?
Article: Gaussian graphical models with applications to omics analysesAuthors and Year: Katherine H. Shutta, Roberta De Vito, Denise M. Scholtens, Raji Balasubramanian 2022Journal: Statistics in Medicine Review Prepared by: Sanou Edmond, Postdoc in BiostatisticsNuclear Safety and Radiation Protection Authority (ASNR) As scientists collect more detailed biological data, they use networks to understand how molecules in the body interact and how these interactions relate to disease. This type of data, known as omics, includes information about genes (genomics), proteins (proteomics), and other molecules. These networks can help find genes linked to illness and even suggest possible treatment options. Statisticians help by using tools that highlight which molecules are directly connected. In their tutorial “Gaussian Graphical Models with Applications to Omics Analyses,” Shutta et al. recommend using a method called Gaussian Graphical Models (GGMs) to study these connections. GGMs help draw simple, clear maps of how molecules relate to each other. The authors…
Directional weirdness: when statistical depth runs out of depth
Article: Directional Outlyingness for Multivariate Functional DataAuthors and Year: Wenlin Dai & Marc G. Genton 2019Journal: Computational Statistics & Data Analysis Review Prepared by: Moinak BhaduriDepartment of Mathematical Science, Bentley University, Massachusetts Outliers are individuals and entities to whom we have forever turned with awe and skepticism, with curiosity and suspicion, with expectation and anxiety. They do not fit the norm and are, oftentimes, for better or for worse, risky to ignore. Malcolm Gladwell in his book Outliers: The story of Success samples our society and brings out such remarkable individuals and examines commonalities: what thread binds them, what makes them deviate from the crowd. And just as a common tendency is difficult to pinpoint while investigating these people – some were forced to the extremes by social pressure or hardships, while some others are propelled by sheer curiosity – statistical data which are more complex than simple numbers, may…
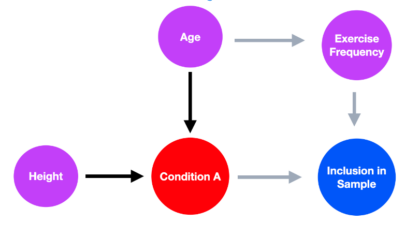
Understanding how selection bias impacts our ability to learn from health data
Article Title: A framework for understanding selection bias in real-world healthcare data Authors & Year: R. Kundu, X. Shi, J. Morrison, J. Barrett, and B. Mukherjee (2024)Journal: Journal of the Royal Statistical Society Series A: Statistics in SocietyReview Prepared by Peter A. Gao Electronic health record (EHR) databases compile hundreds of thousands, or even millions, of patients’ medical histories, enabling researchers to study large populations and observe how their health evolves over time. The databases present an opportunity to identify risk factors for certain diseases, evaluate the efficacy of treatments for people of different backgrounds, and map health disparities. However, individuals are rarely included in such datasets at random, meaning the observed sample may not be representative of the target population. If certain groups are underrepresented in EHR data, using it to measure the prevalence of a condition or to assess the association between a risk factor and a condition…
Generative A.I. in SPC: Unlocking New Potential while Tackling the Risks
Title: How generative AI models such as ChatGPT can be (mis)used in SPC practice, education, and research? An exploratory studyAuthors & Year: Megahed, F.M., Chen, Y.J., Ferris, J.A., Knoth, S., and Jones-Farmer, L.A. (2023)Journal: Quality Engineering [DOI:10.1080/08982112.2023.2206479]Review Prepared by David Han Statistical Process Control (SPC) is a well-established statistical method used to monitor and control processes, ensuring they operate at optimal levels. With a long history of application in manufacturing and other industries, SPC helps detect variability and maintain consistent quality. Tools like control charts play a central role in identifying process shifts or trends, allowing timely interventions to prevent serious defects. Megahed, et al. (2023) explores how generative AI, particularly ChatGPT, can enhance the efficiency of SPC tasks by automating code generation, documentation, and educational support. While AI shows promise for routine tasks, the study also highlights its limitations in handling more complex challenges. For instance, ChatGPT’s misunderstanding of…
A promising way to disentangle time from space kicks off
Review Prepared by: Moinak Bhaduri Mathematical Sciences, Bentley University, Massachusetts Fine! I admit it! The title’s a bit click-baity. “Time” here need not be some immense galactic time. “Space” refers here not to the endless physical or literal space around you, but more to the types of certain events. But once you realize why the untangling was vital, how it is achieved in games such as soccer, and what forecasting benefits it can lead to, you’ll forgive me. You see, for far too long, whenever scientists had to model (meaning describe and potentially, forecast) phenomena that had both a time and a value component, such as the timing of earthquakes and magnitude of those shocks, or times of gang violence and casualties because of those attacks, their default go-to were typical spatio-temporal processes such as the marked Hawkes (described below). While with that reliance no fault may be found in…
Data Fission – Statistical Analysis through Data Point Separation
Title: Data Fission: Splitting a Single Data PointAuthors & Year: J. Leiner, B. Duan, L. Wasserman, and A. Ramdas (2023)Journal: Journal of the American Statistical Association[DOI:10.1080/01621459.2023.2270748]Review Prepared by David Han Why Split the Data? In statistical analysis, a common practice is to split a dataset into two (or more) parts, typically one for model development and the other for model evaluation/validation. However, a new method called data fission offers a more efficient approach. Imagine you have a single data point, and you want to divide it into two pieces that cannot be understood separately but can fully reveal the original data when combined. By adding and subtracting some random noise to create these two parts, each part contains unique information, and together they provide a complete picture. This technique is useful for making inferences after selecting a statistical model, allowing for better flexibility and accuracy compared to traditional data splitting…
Unveiling the Dynamics of Human-AI Complementarity through Bayesian Modeling
Article Title: Bayesian modeling of human–AI complementarity Authors & Year: M. Steyvers, H. Tejeda, G. Kerrigan, and P. Smyth (2022) Journal: Proceedings of the National Academy of Sciences of the United States of America [DOI:10.1073/pnas.2111547119] Review Prepared by David Han Exploration of Human-Machine Complementarity with CNN In recent years, artificial intelligence (AI) and machine learning (ML), especially deep learning, have advanced significantly for tasks like computer vision and speech recognition. Despite their high accuracy, these systems can still have weaknesses, especially in tasks like image and text classification. This has led to interest in hybrid systems where AI and humans collaborate, focusing on a more human-centered approach to AI design. Studies show humans and machines have complementary strengths, prompting the development of frameworks and platforms for their collaboration. To explore this further, the authors of the paper developed a Bayesian model for image classification tasks, analyzing predictions from both humans…
The A.I. Doctor is In – Application of Large Language Models as Prediction Engines for Improving the Healthcare System
Predictive Healthcare Analytics
Physicians grapple with challenging healthcare decisions, navigating extensive information from scattered records like patient histories and diagnostic reports. Current clinical predictive models, often reliant on structured inputs from electronic health records (EHR) or clinician entries, create complexities in data processing and deployment. To overcome this challenge, a team of researchers at NYU developed NYUTron, an effective large language model (LLM)-based system, which is now integrated into clinical workflows at the NYU Langone Health System. Using natural language processing (NLP), it reads and interprets physicians’ notes and electronic orders, trained on both structured and unstructured EHR text. NYUTron’s effectiveness was demonstrated across clinical predictions like readmission (an episode when a patient who had been discharged from a hospital is admitted again), mortality (death of a patient), and comorbidity (the simultaneous presence of two or more diseases or medical conditions in a patient) as well as operational tasks like length of stay and insurance denial within the NYU Langone Health System. Reframing medical predictive analytics as an NLP problem, the team’s study showcases the capability of LLM to serve as universal prediction engines for diverse medical tasks.

![Flow chart showing the steps of the LLM approach for clinical prdeiction. The top left is part a with a Lagone EHR box connected to 2 boxes, NYU Notes(clinical notes) and NYU Fine-Tuning (clinical notes and task specific labels). The top right is the pret-training section with NYU notes (clinical notes) in the far top right connected to a language model box which then connects to a larger masked language model box below it (fill in [mask]: a 39-year-old [mask] was brough in by patient (image representing llm replying) patient)). The bottom left has nyu fine tuning (clinical notes and task specific tasks) in the top right of its quadrant connected to a pretrained model box which connects down to a larger fine-tuning box, specifically the predicted p(label) ground truth pair (0.6, 0.4) which connects to a small box inside the big on lageled loss which goes to another small box labeled weight update which goes back to the pretrained model box. The last quadrant in the bottom right has two boxes on the left of fine-tuned model and hospital ehr(clinical notes) connected to inference engine in the top right of the quadrant that connects down to the email alert (physician) box](https://mathstatbites.org/wp-content/uploads/apollo13_images/msbHanNyu1-7ipft2sg6himqf4p6irp5l74aclvk4e4w6.png)