Title: Balanced Excited Random Walk in Two Dimensions
Authors and Year: Omer Angel, Mark Holmes, Alejandro Ramirez; 2023
Journal: Annals of Probability
Will balance and excitement always lead a random walker home? A new paper in the Annals of Probability attempts to answer this question and explores paths along the way.
Random Walks
Imagine you moved into a new neighborhood and you are excited to go on a walk to explore. The neighborhood is arranged in a grid structure, so at each intersection you have four choices for which direction to take: left, right, forwards, or backwards. Since you don’t know where you’re going, you decide to use some randomness to pick which direction to take. This is a random walk: a type of random process that is just a succession of steps on some sort of graph according to some probabilistic rules. The neighborhood grid gives a walk in two dimensions, because at each intersection you can go forward/backward or left/right.
In a balanced random walk, every direction has the same probability – there is always a ¼ chance each that you go left, right, forward, or backward. You could flip a coin to first decide whether to move in the forward/backward or left/right direction, and then flip it again to decide which of the two options to take. In an excited random walk, the first time you visit an intersection there is some bias in one direction – maybe you know that the cool park is somewhere to the left, so you always try that at a new intersection – but on future visits to the intersection you go back to the rule that every direction has the same probability.
The balanced excited random walk combines these two ideas. Maybe you’ve decided that instead of exploring everything completely randomly, you want to be more strategic to try to cover more ground. Now, the first time you reach a new intersection, you flip a coin to decide whether to keep going straight or turn around, but whenever you reach an intersection you recognize, you flip a coin to decide to turn left or right. Figure 1 shows one simulation of this random process, which tracks the path of a balanced excited random walker starting from (0, 0) on the grid.
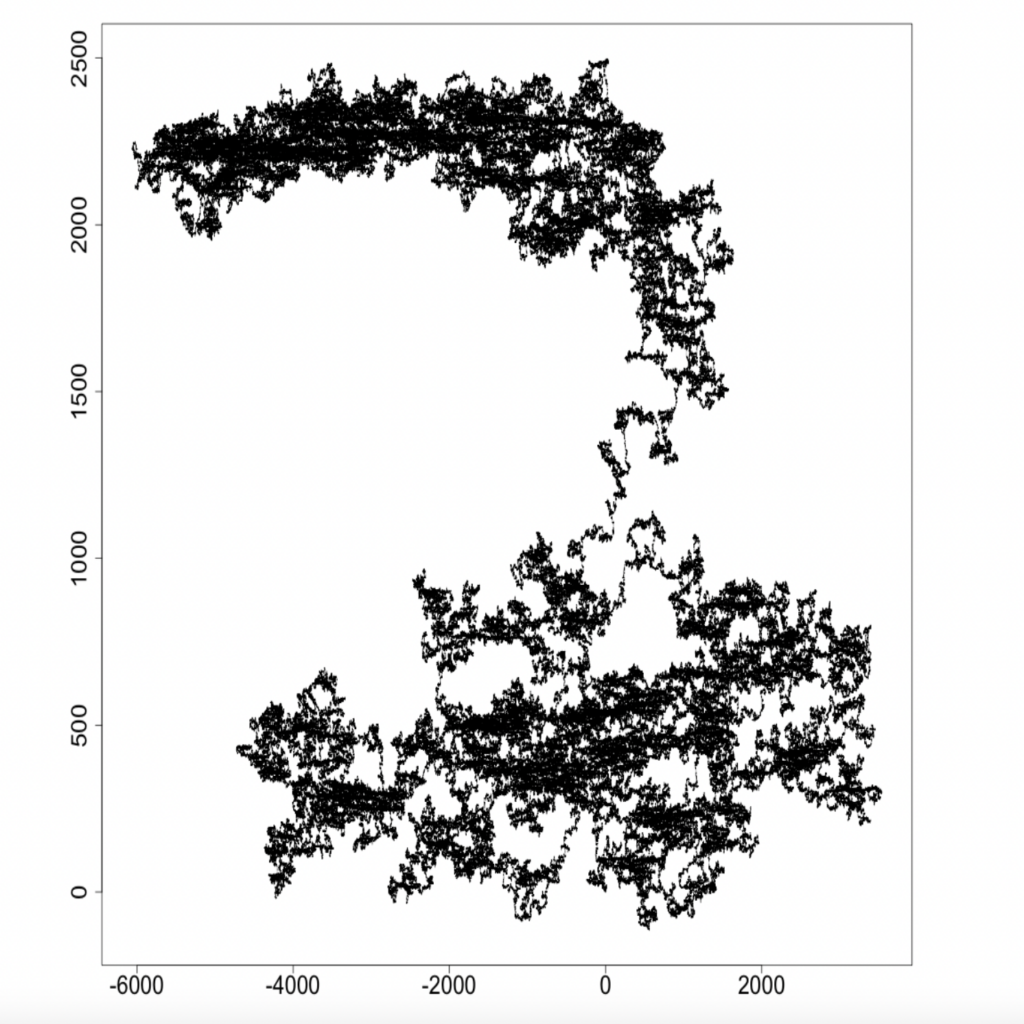
Figure 1: A simulation of the 2-dimensional excited balanced random walk after 108 steps.
Returning Home
Let’s suppose that your new neighborhood is infinite! You could keep on walking forever … What are the odds of eventually returning home to where you started? Perhaps at the beginning you circle back and return to where you started, but eventually you head off in some direction and never return again. This property of a random walk is called transience – the walk returns to its starting point only a finite number of times. In contrast, recurrence means that the walk returns to its starting point infinitely many times.
It’s not obvious whether a random walk is always recurrent or transient. Consider the balanced random walk (remember, at each step every direction is equally likely). In one dimension, there are only two choices for each step, either forwards or backwards – imagine moving up and down an infinite ladder. In this case, the random walk is always recurrent. The balanced random walk is also recurrent in two dimensions, like walking on the neighborhood grid. However, in three dimensions (now you could go left-right, forward-back, or up-down), the random walk is transient.
What about the balanced excited random walk? The balanced random walk is a special type of random process called a Markov chain. This means that the probability of the walker’s position at the next step only depends on its current position. Maybe the walker happened to take 10 steps to the right in a row; this past history doesn’t matter, there is still the same chance of moving to the right at the next step. However, the balanced excited random walk does not have this property. Your probability of taking a step at a given position does depend on your past, because it matters whether or not you’ve visited this position before. This makes the balanced excited random walk much more difficult to study.
Some Findings
The conjecture is that in two dimensions the balanced excited random walk is always recurrent, just like the balanced random walk. The authors of the paper “Balanced Excited Random Walk in Two Dimensions” prove that the set of recurrent sites (the sites which are visited infinitely many times) is either everything or nothing. The next question is, is the set of recurrent sites always either everything or nothing? It could be possible that you set out on a balanced excited random walk and you will visit every site infinitely often, but your friend set out on their own walk and will head off in some direction so they will visit every site only a finite number of times.
The authors also prove a result about how the total number of sites visited by the random walk grows as the total number of steps grows. This still leaves much to be studied, but it is a first step to understanding the balanced excited random walk in two dimensions.
More to Explore
Random walks are used to study randomness in many areas. For example, mutations accumulating randomly in DNA, users randomly exploring webpages, or neurons firing in the brain. Different types of random walks are needed to model different scenarios and understanding the long-term properties is important mathematically and in applications.
The balanced excited random walk is a non-Markov process and still poses many unanswered questions. Mathematicians will need to keep on walking to explore the mysteries of this random process.

![Flow chart showing the steps of the LLM approach for clinical prdeiction. The top left is part a with a Lagone EHR box connected to 2 boxes, NYU Notes(clinical notes) and NYU Fine-Tuning (clinical notes and task specific labels). The top right is the pret-training section with NYU notes (clinical notes) in the far top right connected to a language model box which then connects to a larger masked language model box below it (fill in [mask]: a 39-year-old [mask] was brough in by patient (image representing llm replying) patient)). The bottom left has nyu fine tuning (clinical notes and task specific tasks) in the top right of its quadrant connected to a pretrained model box which connects down to a larger fine-tuning box, specifically the predicted p(label) ground truth pair (0.6, 0.4) which connects to a small box inside the big on lageled loss which goes to another small box labeled weight update which goes back to the pretrained model box. The last quadrant in the bottom right has two boxes on the left of fine-tuned model and hospital ehr(clinical notes) connected to inference engine in the top right of the quadrant that connects down to the email alert (physician) box](https://mathstatbites.org/wp-content/uploads/apollo13_images/msbHanNyu1-7ipft2sfku393xh5nv4pp16roldxrt3aay.png)