Title: Bayesian Light Source Separator (BLISS)
Authors: Jeffrey Regier and Ismael Mendoza
Conference: Statistical Challenges in Modern Astronomy VIII
What is SCMA8?
In June 2023, astronomers and statisticians flocked to “Happy Valley’” Pennsylvania for the eighth installment of the Statistical Challenges in Modern Astronomy, a bidecadal conference. The meeting, hosted at Penn State University, marked a transition in leadership from founding members Eric Feigelson and Jogesh Babu to Hyungsuk Tak, who led the proceedings. While the astronomical applications varied widely, including modeling stars, galaxies, supernovae, X-ray observations, and gravitational waves, the methods displayed a strong Bayesian bent. Simulation based inference (SBI), which uses synthetic models to learn an approximate function for the likelihood of physical parameters given data, featured prominently in the distribution of talk topics. This article features work presented in two back-to-back talks on a probabilistic method for modeling (point) sources of light in astronomical images, for example stars or galaxies, delivered by Prof. Jeffrey Regier and Ismael Mendoza from the University of Michigan-Ann Arbor.
One star two star, red star blue star?
In analyzing an image of a given patch of sky, astronomers often want to know: How many stars are there? What are the locations of those stars? How bright are they? What color (relative brightness in one wavelength versus another) are they? However, measuring even the simplest of these properties can become complicated in “crowded” fields, where lots of stars appear close together on the “plane of the sky,” our 2-dimensional view of the universe that we see in images. How do we distinguish the case of two stars that appear nearly on top of each other from a single brighter star?
Another common “source” of light in these images are galaxies outside of the Milky Way. Most of these galaxies are so distant that we cannot see small filaments and clusters within the galaxies (like we can with the impressive images of nearby Andromeda). However, astronomers still want to measure additional properties of galaxies such as rough shape information, for instance via the Sérsic profile that measures brightness as a function of radius from the galaxy’s center. As our instruments and telescopes improve, astronomical images include dimmer and more distant galaxies. This only compounds the problem of “crowding” since by probing out to further distances, we see more galaxies per square degree of the plane of the sky. Further, such distant galaxies can often appear so point-like that they are hard to distinguish from stars, making “Is it a star or galaxy?” another difficult question in the image analysis.
One way to address the problem of reporting a large number of often uncertain properties for a source is to infer a probability distribution for the source having a certain value for that property (being a star/galaxy, having a certain color, etc.). But, that assumes a list of known sources that have some properties and does not account for an uncertainty with respect to the number of sources! Inferring a probability distribution in this regime with an unknown number of unknowns is more complicated and is called “transdimensional inference.” In our example, this means that the result of the inference is a set of possible lists of sources (locations and properties), and each of those lists, which may have a different number of sources, has a probability attached to it.
Enter the Bayesian Light Source Separator (BLISS)!
The Bayesian Light Source Separator (BLISS) method presented by Regier and Mendoza is an example of one such transdimensional inference pipeline, a schematic of which is shown in Figure 1. BLISS uses neural networks to act as “encoders” taking in images and outputting probability distributions. The first encoder creates a probability distribution over the number of sources and their locations within a given sub-image. Cutout images centered on those locations are fed to subsequent “encoders” to measure properties of those proposed sources (probability of being a galaxy or a star, brightness, etc.). Finally, a neural network acting as a “decoder” takes a given catalog (list of sources and source properties) and creates a noiseless model image which can be compared to the real image.
Figure 1. Schematic of the probabilistic detection and measurement of light sources in an astronomical image performed by the Bayesian Light Source Separator (BLISS) (Adapted from Hansen et al., Figure 1).
Regier’s talk focused on some of the major improvements in BLISS over similar previous methods (such as Celeste). One major change was switching the measure of success used when training the neural networks (“encoder”/”decoder”) from the reverse to forward Kullback-Leibler (KL) divergence. The KL divergence is a measure of how different two probability distributions are and is defined below.
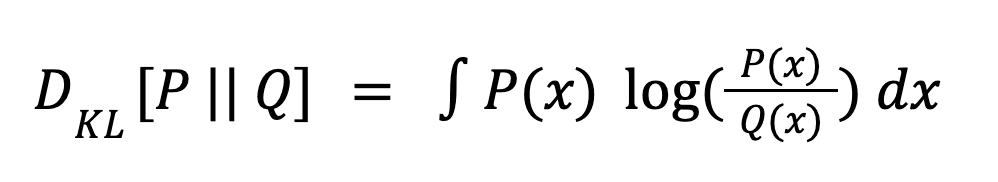
When P represents the true distribution and Q is an approximation to the truth, for example the outputs of the neural networks learned by BLISS, the formula above is called the “forward” KL divergence. The same equation with P and Q switched is called the “reverse” KL divergence.
Figure 2 helps illustrate the difference between them. The forward KL is sensitive to regions where the true distribution P ≠ 0 while the reverse KL is sensitive to regions where the approximate distribution Q ≠ 0. The approximation Q in the right panel is heavily disfavored by the forward KL because Q ≈ 0 in regions where P ≠ 0, and hence incurs a large penalty from the log term in contrast to the approximation Q in the left panel. However, in the right panel, Q is a better approximation to P where Q ≠ 0 and is thus preferable under the reverse KL, which has no penalty where Q = 0. This “mode covering” behavior shown in Figure 2 (left) helps give intuition for Regier’s result that the forward KL performs better at the highly multimodal task of source separation.
Figure 2. Examples of distributions Q approximating the true distribution P that are preferred under forward KL (left) versus reverse KL (right). (Figure inspired by blog post)
Aspirations for a State of BLISS
The pair of researchers showed exciting progress toward several extensions of the model to handle multiband images (images containing information from multiple different wavelengths), image coaddition (combining multiple different images of the same location taken at different times), and variability in the point spread function (which describes how changes in the atmosphere or telescope can impact the image). Some limitations of BLISS were discussed, mostly centered around the current scheme for subdividing the image into smaller regions for processing. Mitigating these shortcomings and demonstrating BLISS on a diverse and large number of real images, which can often be “messy,” are the next steps as the BLISS team sets its sights on processing the deluge of data from the Legacy Survey of Space and Time (LSST) at Vera C. Rubin Observatory which is starting observations next year.
Figures used with permission from the authors.
